Juhongyee

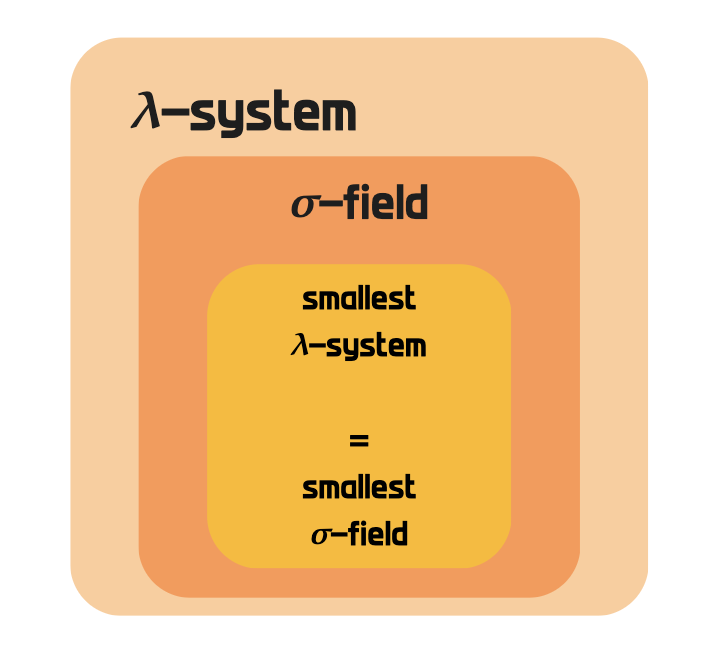
서론푹 찍 확률론 세번째 글입니다. 이번엔 Dynkin's $\pi - \lambda$theorem인데 이전에 아래의 찍먹 측도론 포스팅에서 다룬 적이 있습니다.https://juhongyee.tistory.com/30 찍먹 측도론 3 Dynkin $\pi - \lambda$ theorem(Dynkin Pi-lambda theorem)서론지난 시간에는 Carathéodory's extension theorem에 대해 알아보았습니다. 그런데 이 정리에서 $\sigma$-finite라는 조건을 추가했을 때는 그 measure가 unique 하게 존재합니다.이는 Probability measure에서 일반juhongyee.tistory.com매우 중요한 정리이기 때문에 확률론에서 다른 notation들로 또 ..

서론본 포스팅은 서울대학교 대학원 통계학과 확률론1 과목 내용을 포함합니다.교재로는 Durrett, R. (2019). Probability: Theory and Examples (5th ed.). Cambridge University Press 을 참고합니다. 지금까지 와의 포스팅과 다르게 정리들을 간단하게 정리하고 설명하는 형식으로 포스팅될 예정입니다. 시작하겠습니다. 본론Measure Theory가 아닌 Probability Theory이기 때문에 Measure에 관해 심도 있게 다루지는 않습니다. 1. Def of probability spaceA probability space is a triple $(\Omega, \mathcal{F}, P)$where $\Omega$ is a set of "..

서론본격적으로 3월에 입학하기 전 통계학과에서 막 수학 공부를 시켜주는게 있다.이름하야 매스부트캠프. 엄청난 속도로 수학 진도를 나간다는 소문만 들었는데 오늘 그 첫 수업을 들었다. 그나마 조금 알고 있던게 도움은 됐는데 복습을 한 번 해보자.이 글은 진짜 그냥 생각나는대로 이해한대로 휘갈겨 쓰는 글이 될 것으로 예상한다. 본론1. Measure Theory시작부터 측도론이다. 지난 번에 찍먹 측도론 글을 올린게 도움이 됐다.1.1 Introduction먼저 Riemann integrable에 대해 다뤘다. Riemann integrable한 것은 뭐 먼저 [a,b]에 Partition을 주는 걸로 시작한다. 아마 [a,b]인 이유는 Heine-Borel에 의해 compact set이고 compact s..

서론누적분포함수(c.d.f)란 무엇일까요?처음 배울 땐 이 개념이 참 막막했습니다. 누적분포함수를 확률밀도(or 질량)함수의 적분 정도로 생각했기 때문입니다.이게 대체 뭐가 중요한건지, 왜 알아야하는건지 잘 몰랐습니다. 그런데 수리통계학을 공부하며 하나하나 알아가보니 생각보다는 쉬웠던 것 같습니다.이번 시간에는 함께 누적분포함수의 정의와 성질을 알아보면서 이것이 무엇인지 알아가봅시다. 본 포스팅은 Statistical Inference(2rd, George Casella, Roger L. Berger) 및 수리통계학(2012, 김우철)의 내용을 참고하였습니다.본론본론에서는 누적분포함수를 cdf, 확률밀도함수를 pdf라고 하겠습니다. 확률밀도함수 pdf와 누적분포함수 cdf는 확률변수가 어떤 분포를 따르는..

서론지난 시간에는 Carathéodory's extension theorem에 대해 알아보았습니다. 그런데 이 정리에서 $\sigma$-finite라는 조건을 추가했을 때는 그 measure가 unique 하게 존재합니다.이는 Probability measure에서 일반적인 상황입니다. 그렇다면 한 번 증명해봐야겠죠? 이 uniqueness를 증명하기 위한 초석은 Dynkin $\pi - \lambda$ theorem을 증명하는 것입니다.이를 위해 $\pi$ system과 $\lambda$ system에 대해서도 차근차근 알아보죠! 본론Definition of $\pi$ system$\pi$ system의 정의부터 찬찬히 알아봅시다. 다음은 그 서술입니다.A collection of $\mathcal{A..

서론오늘은 Carathéodory's extension theorem에 대해 알아보겠습니다. (완벽 증명) 이 정리는 정말 좋은 정리인데요! Ring에서 pre-measure를 잘 정의하면 이를 mesure로 잘 확장할 수 있다는 뜻입니다.  이 정리의 필요성에 대해 생각해 봅시다.어떤 $\Omega$의 $\mathcal{P} (\Omega)$에 대해 measure가 쉽게 정의되지 않습니다. Lebesgue measure에 대해 Vitali set을 생각해 보면 직관적으로 존재해야 할 것 같은 measure에도 그 값이 존재하지 않을 수 있죠. 그런데 Carathéodory's extension theorem은 이런 경우를 배제하고 measure가 잘 존재하도록 하는 방법에 대해 알려줍니다.한 번 그 과..

서론확률 측도(Probability Measure)가 대체 무엇일까 고민하던 나날 중 측도론(Measure Theory)를 공부해야겠다는 마음을 먹었습니다. 시간이 많이 않기 때문에 핵심만 훑으면서 일주일컷을 내려고 했지만... 진짜 대충만 알게 됐습니다 ㅋㅋㅋㅋ 그래도 아는 것 범위 내에서는 이해한 것 같아서 기록을 남겨두려 합니다. 본 포스팅은 https://www.youtube.com/@cachelackmathstatslectures7001 강의를 듣고 이해한 바를 중심으로 하고 있습니다. 본론일단 2024/07/04, 이 글을 쓰는 첫 날에 제가 이해하지 못하거나 아직 모르는 것을 서술해 보겠습니다. 1. Measureable의 직관적 정의Measureable의 정의가 다음과 같은데요.Set $A..