1. 조건부 확률

서론

correlation이란 무엇인지 알기 위한 여정 첫 번째는 조건부확률이다. 조건부확률은 조건이 달려있을 때의 확률이라는 것인데 어떻게 구할 수 있을까?
간단하게 알아보자.

조건부확률

정의

조건부확률이란 어떤 사건 B가 일어났을 때 A가 일어날 확률을 의미하는 것으로 $$P(B|A)$$로 쓴다.

$P(B|A) =$$P(A∩B)\over P(B)$와 같이 쓸 수 있다.

왜? $P(A|B) =$$P(A∩B)\over P(B)$

가장 기저의 개념을 생각해보자. 사건 A가 일어날 확률이란 일어날 수 있는 모든 사건들이 모여 있는 전체집합이 있어 일어날 수 있는 전체 사건들 중 A가 일어날 비율을 의미하는 것이다.

즉 S를 전체집합이라고 한다면 A가 일어날 확률은 $n(A)\over n(S)$인 것이다. n은 집합의 개수.
$n(A)\over n(S)$ = (A가 일어나는 경우에 대한 집합의 개수)/(S의 집합의 개수)

그러면 $P(A|B)$는 B가 일어나는 경우 중 따져야겠네. 즉 B가 전체집합이 되는 것과 비슷하다. 이 B가 일어날 때 A가 일어난다는 것은 B와 A가 동시에 일어난다는 의미이고 즉, B와 A의 교집합이 되어야한다.
즉.B가 일어나는 경우의 수가 $n(B)$, A와 B가 동시에 일어나는 경우의 수가 $n(A∩B)$

$\frac{n(A∩B)}{n(B)} = \frac{n(A∩B)\over n(S)}{n(B)\over n(S)} = \frac{P(A∩B)}{P(B)}$

결론)B를 전체집합으로 가정하여 그 안에 A가 몇 번 일어나는지에 관한 비율과 같다.

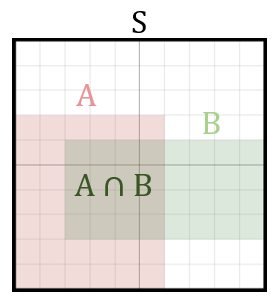
시각화

나무위키에 좋은 설명 그림이 있어 가져왔다.

https://namu.wiki/w/%EC%A1%B0%EA%B1%B4%EB%B6%80%ED%99%95%EB%A5%A0