서론
지난 시간에는 Carathéodory's extension theorem에 대해 알아보았습니다. 그런데 이 정리에서 $\sigma$-finite라는 조건을 추가했을 때는 그 measure가 unique 하게 존재합니다.
이는 Probability measure에서 일반적인 상황입니다. 그렇다면 한 번 증명해봐야겠죠?
이 uniqueness를 증명하기 위한 초석은 Dynkin $\pi - \lambda$ theorem을 증명하는 것입니다.
이를 위해 $\pi$ system과 $\lambda$ system에 대해서도 차근차근 알아보죠!
본론
Definition of $\pi$ system
$\pi$ system의 정의부터 찬찬히 알아봅시다. 다음은 그 서술입니다.
A collection of $\mathcal{A}$ is a $\pi$ - system if $\forall A,B \in \mathcal{A}$ then $A \cap B \in \mathcal{A}$ and $\varnothing \in \mathcal{A}$
간단하죠? 교집합과 공집합이 $\mathcal{A}$에 속하면 $\pi$ system입니다. ring의 하위호환으로 union은 성립하지 않아도 됩니다.
Definition of $\lambda$ system
이번엔 $\lambda$ system의 정의입니다.
A collection of subsets $\mathcal{L}$ is a $\lambda$ system if
- $\Omega \in \mathcal{L}$
- $A,B \in \mathcal{L}$ s.t if $A \subset B$ then $B-A \in \mathcal{L}$
- if $\{A_i\}_{i=1}^{\infty}$ pairwise disjoint, $A_i \in \mathcal{L}$, the $\bigcup_{i=1}^{\infty} A_i \in \mathcal{L}$
굉장히 $\sigma$ - field와 비슷하죠? 하지만 다른 점이 있습니다. 두 번째를 자세히 보시면 차집합에 대해 닫혀있는 게 아닙니다. 부분집합인 경우 차집합이 $\mathcal{L}$에 속하는 거죠.
또 세 번째의 pairewise 부분에서도 겹치지 않을 때의 countable union만 $\lambda$ system에 속합니다.
이 지식들을 토대로 Dynkin $\pi - \lambda$ theorem을 증명해 봅시다.
Dynkin $\pi - \lambda$ theorem
일단 이 정리가 무엇인지 알아야겠죠.
Let $\mathcal{A}$ be a $\pi$ system, $\mathcal{L}$ be a $\lambda$ system.
And $\mathcal{A} \subseteq \mathcal{L}$. Then $\sigma (\mathcal{A}) \subseteq \mathcal{L}$
$\mathcal{A}$가 $\pi$ system이며 $\lambda$ system에 속한다면 그 generated $\sigma$-field도 $\mathcal{L}$에 속한다는 의미입니다. 원래 $\sigma$-field는 유일하지 않지만 가장 작은 $\sigma$-field는 유일합니다. 가장 작다(smallest)의 정의는 아래에서 보이겠습니다.
자 증명해 봅시다.
proof of Dynkin $\pi - \lambda$ theorem
먼저 $\mathcal{L_0}$가 smallest $\lambda$ system s.t $\mathcal{A} \subset \mathcal{L_0}$라고 해봅시다.
smallest?
그러면 여기서 $\mathcal{A}$를 포함하는 smallest의 정의를 알 필요가 있습니다.
이의 정의는 $\mathcal{A}$를 포함하는 모든 $\lambda$ system의 교집합입니다. 그러면 다시 질문이, $\lambda$ system의 교집합은 교집합인지 생각해 봐야겠죠.
$\mathcal{L_0} = \bigcap_{\mathcal{L}} \mathcal{L}$이 $\lambda$ system인지 알아봅시다. $\lambda$ system의 정의를 따라가면 됩니다.
- 일단 $\Omega \in \mathcal{A}$는 자명합니다. 모든 $\mathcal{L}$이 $\Omega$를 가지고 있기 때문입니다.
- 다음은 차집합인데, $A,B$가 $\mathcal{L_0}$에 속한다고 해보죠. 그러면 모든 $\mathcal{L}$에 $A,B$가 속해있었다는 뜻입니다. 그러면 모든 $\mathcal{L}$들은 $\lambda$ system의 정의에 의해 $A-B$도 가지고 있었습니다. 그러므로 그들의 교집합인 $\mathcal{L_0}$도 $A-B$를 가집니다.
- countable union도 위와 정확히 동일한 원리로 성립합니다.
즉, $\mathcal{L_0}$가 잘 존재하여 우리가 선택할 수 있습니다.
($\mathcal{L}$ s.t $\mathcal{A} \subset \mathcal{L}$의 존재성에 대해 더 고려할 점이 있지만 별 거 아니므로 패스하겠습니다.)
다시 본 증명으로 돌아옵시다.
우리의 목표는 $\mathcal{L_0}$가 $\pi$ system이라는 것과, $\pi$ system과 $\lambda$ system을 동시에 만족하는 set의 집합은 $\sigma$ field임을 보이는 것입니다.
결국 $\sigma (\mathcal{A}) \subseteq \mathcal{L_0} \subseteq \mathcal{L}$을 보이고자 합니다.
step1 Show that $\mathcal{L_0}$ is contains all intersections with element of $\mathcal{A}$
먼저 $\mathcal{L'} = \{B \in \mathcal{L_0} : B \cap A \in \mathcal{L_0}, \forall A \in \mathcal{A}\}$ 을 정의합시다.
먼저 $\mathcal{L_0}$는 $\mathcal{A}$를 포함한다는 걸 기억합시다. 그러면 $\mathcal{L'}$은 최소 $\mathcal{A}$는 포함하겠죠. 왜냐하면 $A \in \mathcal{A}$들은 $\mathcal{A}$가 $\pi$ system이므로 정의를 만족합니다.
즉, $$\mathcal{A} \subset \mathcal{L'}$$입니다.
자, 이제 $\mathcal{L'}$이 $\lambda$ system임을 보여봅시다.
$\lambda$ system의 정의를 하나하나 체크합시다.
- 일단 $\Omega$를 당연히 포함합니다. $\mathcal{A}$를 부분집합으로 가지고 있기 때문입니다.
- $B_1,B_2 \in \mathcal{L'}$ 이고 $B1 \subset B2$라고 합시다. 그러면 $\mathcal{L'}$의 정의에 의해 $B_1 \cap A, B_2 \cap A \in \mathcal{L_0}$입니다.
그렇다면 $(B_1 \cap A) - (B_2 \cap A) = (B_2 - B_1) \cap A \in \mathcal{L_0}$가 만족함을 쉽게 보일 수 있습니다. $B_1$이 $B_2$의 부분집합이고, 각각이 $\mathcal{L_0}$에 속하므로 그 차도 $\mathcal{L_0}$에 속합니다..
즉, $$\therefore B_2-B_1 \in \mathcal{L'}$$입니다.
- $\{B_i\}_{i=1}^{\infty} \in \mathcal{L'}$ 이고 pairwise disjoint라고 해봅시다.(또 $A \in \mathcal{A}$)
그러면 $\mathcal{L'}$의 정의에 따라 $A \cap B_i \in \mathcal{L_0}$임을 활용해보면$\bigcup_{i=1}^{\infty} (A \cap B_i) \in \mathcal{L_0}$겠죠? $\lambda$ system의 세 번째 정의에서 $B_i$가 pairwise disjoint하기 때문에 위 문장이 성립합니다.
즉, $\bigcup_{i=1}^{\infty} (A \cap B_i) = A \cap \bigcup_{i=1}^{\infty} B_i$이므로 $A \cap \bigcup_{i=1}^{\infty} B_i$도 $\mathcal{L_0}$에 속하게 됩니다.
그러므로 $\mathcal{L'}$의 정의에 따라 $$\bigcup_{i=1}^{\infty} B_i \in \mathcal{L'}$$입니다.
즉, $\mathcal{L'}$은 $\lambda$ system인데요. 정의에 따라 $\mathcal{L'} \subset \mathcal{L_0}$겠죠? $\mathcal{L_0}$ 내에서 택하여 $\mathcal{L'}$을 만들었으니까요. 그런데 다시 $\mathcal{L_0}$는 minimal, 즉, 가장 작은 $\lambda$ system입니다. 이로부터, $$\mathcal{L'} = \mathcal{L_0}$$임을 알 수 있겠습니다.
step2 Show that $\mathcal{L_0}$ is closed under intersection
이번엔 $\mathcal{L''} = \{B \in \mathcal{L_0} : B \cap A \in \mathcal{L_0}, \forall A \in \mathcal{L_0}\}$ 을 정의합시다.
그렇다면 $\mathcal{L_0}$에 $\mathcal{A}$가 속하기 때문에, $\mathcal{L'}$의 정의에 따라 $\mathcal{L'} = \mathcal{L_0} \subset \mathcal{L''}$이 성립합니다.
이때, $\mathcal{L''}$은 $\mathcal{L_0}$에서 택하여 정의했기 때문에 $\mathcal{L''} \subset \mathcal{L'}$입니다.
즉, $\mathcal{L''} = \mathcal{L_0}$이고, $\mathcal{L_0}$ 는 closed under intersection이라고 할 수 있겠습니다.
step3 proof by using the fact that collection of sets that is both $\lambda$ and $\pi$ system is $\sigma$-field
우리는 정의를 통해 $\lambda$ system이고 $\pi$ system 이면 $\sigma$-field임을 알 수 있습니다.
즉 $\mathcal{L_0}$가 $\sigma$-field임을 알 수 있죠.
그런데 모든 $\sigma$-field는 $\lambda$ system이므로 가장 작은 $\lambda$ system이 $\pi$ system이기까지 하니 $\mathcal{L_0}$(smallest)는 $\sigma (\mathcal{A})$(smallest)가 됩니다.
즉, $\sigma(\mathcal{A}) \subseteq \mathcal{L}$입니다.
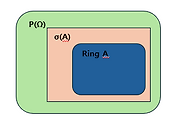
그림으로 표현해 보면 아래와 같습니다.

결론
$\sigma(\mathcal{A}) \subseteq \mathcal{L}$라는 좋은 결과를 얻어냈는데 이는 measure의 uniquness를 증명할 때 쓰입니다!
사실 $\sigma(\mathcal{A})$의 의미를 글을 쓰는 중간까지도 잘못 알고 있었어서 고생을 좀 했습니다.
다음 포스팅은 uniqueness를 증명해 보겠습니다. 그런데 이제는 시간이 좀 부족해서 나중에나 올릴 것 같네요!
그럼 다음에 뵙겠습니다ㅏㅏ
'수리통계를 위한 해석학' 카테고리의 다른 글
| 해석학 정리 2 수열의 극한 예제 문제 풀이2-1(Bartle and Sherbert) (0) | 2025.02.03 |
|---|---|
| 해석학 정리 1 수열의 극한 예제 문제 풀이1(Bartle and Sherbert) (0) | 2025.02.02 |
| 찍먹 측도론2 Carathéodory's extension theorem and proof (0) | 2024.07.08 |
| 찍먹 측도론 Introduction(measure theory) (0) | 2024.07.05 |
| Moment Generating Function의 미분가능성? 3(feat. Power Series) (0) | 2024.06.23 |