서론
이 글은 power series의 미분가능성을 해석학적으로 알아보는 두번째 글입니다. 이 글을 통해 m.g.f가 어째서 미분 가능하고 우리가 잘 적률을 구할 수 있는지 결론을 얻어봅시다.
이전 글에서는 Uniform Convergence의 개념과 Cauchy Criterion에 대해 알아보았습니다.
이번 글에서는 이들을 활용하여 power series의 uniformly convergent에 대해 알아봅시다.
더불어 일반적인 sequence of functions의 미분가능성(differentiability)를 확인해봅시다.
본 포스팅은 Principles of Mathematical Analysis.3rd(Rudin)을 참고하고 있으며 서적에서 다루는 증명을 해설합니다.
본론
Weierstrass M test
sum of functions를 수렴성을 판단하는데에는 정말 유명한 정리가 존재합니다.
바로바로 Weierstrass M test 입니다.
Weierstrass M test는 function $f_n$이 $M_n$에 대해 bound 되고 $\sum_{n=0}^{\infty} M_n$이 수렴한다면 함수 $\sum_{n=0}^{\infty} f_n(x)$가 uniformly converge한다는 의미입니다!
그러니까 함수의 bound를 쉽게 찾고 그의 sum이 수렴함을 보일 수 있다면 함수의 sum이 uniformly converge함은 따라옵니다.
정의 Rudin thm 7.10
Suppose ${f_n}$ is a sequence of functions defined on $E$, and suppose $$|f_n(x)| \leq M_n \;(x \in E, n=1,2,3,...)$$.
Then $\sum f_n$ converges uniformly on $E$ if $\sum M_n$ converges.
증명이 매우 쉬워요~ 앞에서 배운 Cauchy Criterion을 사용하면 됩니다.
증명은 더보기에 적어두겠습니다 ㅎ 필요하신 분은 확인해보세요.
증명
$|f_n(x)| \leq M_n$을 만족하는 $M_n$을 잘 찾았다고 합시다.
예를 들어 $\frac{1}{x^2+n^2}$의 $M_n$으로 $\frac{1}{n^2}$를 잡았다고 합시다. x가 무슨 값이던 그 절댓값보다 $\frac{1}{n^2}$이 더 크겠죠?
이 때, $\sum M_n$이 수렴한다고 가정합시다. 여기서 $M_n$은 그냥 수열(sequence)이므로 uniformly converge같은 개념이 없습니다.
sum이 수렴한다는건 지난 포스팅에서 설명했듯 m번째까지의 합으로 만든 새로운 수열이 수렴한다는 의미와 같습니다. 즉 $s_m = \sum_{n=0}^{m}M_n$라는 수열이 수렴하는 것과 같구요. 이제 수열의 수렴의 정의를 사용합시다.
Let $\epsilon > 0$ be given. ㅋㅋㅋ 정말로 많이쓰는 말인데요. $\epsilon$ 하나를 선택했다는 뜻입니다.
그러면 수열의 수렴의 정의에 따라 어떤 자연수 $M$($M_n$아닙니다)이 존재해서 $M$보다 큰 $m$들에 대해 $\sum_{n=0}^{m} M_n \leq \epsilon$ 이 성립할 겁니다.
그런데 지금 $|f_n(x)|$은 $M_n$에 bound되어있기 때문에 $ \sum_{n=0}^{m} |f_n(x)| \leq \sum_{n=0}^{m} M_n \leq \epsilon$ 이라고 할 수 있습니다. 그냥 유한개의 합이니 자명하죠? 더 큰 숫자를 더하는게 항상 더 클겁니다.
자 여기서 과정을 하나하나 봅시다.
1. $ \sum_{n=0}^{m} |f_n(x)| \leq \sum_{n=0}^{m} M_n \leq \epsilon$ 는 확인했구요.
2. $ |\sum_{n=0}^{m} f_n(x)| \leq \sum_{n=0}^{m} |f_n(x)| \leq$ 이 성립합니다. 이건 삼각부등식(triangle inequality)입니다.
3. $ |\sum_{n=t}^{m} f_n(x)| \leq |\sum_{n=0}^{m} f_n(x)|$ 그 어떤 t에 대해서도 이 식이 성립하겠죠?
위의 식들을 하나로 만들어봅시다.
$ |\sum_{n=t}^{m} f_n(x)| \leq \epsilon$을 얻을 수 있죠? t를 앞서 수열의 수렴의 정의에서 선택한 M보다 크게 임의의 것을 선택합시다. 그러면? 이것 이전 포스팅에서 자세히 알아본 Cauchy Criterion을 만족한다는걸 알 수 있습니다.
왜 일까요? sigma의 성질때문이겠죠? $ |\sum_{n=t}^{m} f_n(x)| = |\sum_{n=0}^{m} f_n(x) - |\sum_{n=0}^{t} f_n(x)| = |s_m - s_t| \leq \epsilon$ 이기 때문입니다.
그러므로 $s_m = \sum_{n=0}^{m} |f_n(x)|$ 이 uniformly converge합니다.
위의 Weierstrass M test는 정말정말 유용한 정리입니다. 앞으로 power series의 정리들을 증명할 때도 사용하겠습니다.
Sequence of functions의 미분
미분가능하다는 의미가 무엇일까? 이는 생각보다 단순한데 point a에서 미분가능하다는 것은 $\lim_{n \rightarrow \infty}\frac{f(x)-f(a)}{x-a}$이 존재한다는 뜻입니다. $\frac{f(x)-f(a)}{x-a}$라는 새로운 함수의 극한이 존재하면 된다 뿐이죠. 이것이 갖는 의미는 다음 문제입니다.
그럼 function sequence의 미분 ${f_n'(x)}$이 수렴하는 함수의 미분 $f'(x)$로 수렴할까요?
뭔가 Uniformly converge하면 될 것 같은데 실상은 그렇지 못합니다.
Rudin Example 7.5의 $f_n(x) = \frac{sin(nx)}{\sqrt{n}}$이 그 예시입니다. Uniformly convergent이지만 그의 미분은 수렴하지 못합니다.
그렇기 때문에 Sequence가 어떤 함수로 수렴하고 있을 때 그 미분도 잘 수렴하게 하고 싶다면 어떤 가정을 추가해줘야 합니다.
그 가정은 $f_n'(x)$가 uniformly converge한다는 것입니다.
이건 매우 강력한 가정으로 원래 sequence가 한 점에서만 converge하고 미분이 uniformly converge 하면 원래 함수도 uniformly converge하게 됩니다.
직관적으로 생각해봅시다.
도함수가 정해졌다는건 어디서 증가할지 감소할지에 대한 개형이 정해졌다는 것입니다.
한 점에서의 pointwise converge는 적분상수와 비슷하게 그 위치를 수렴하는 함수의 위치로 정하는 것과 같습니다.
도함수도 정해지고 그 위치도 정해지면서 잘 converge하니 원래 함수도 잘 converge할 것 같네요.
한번 정리를 확인하고 증명도 해봅시다..
Rudin Thm 7.17 미분의 수렴
Suppose ${f_n}$ is a sequence of functions, diffentiable on $[a,b]$ and such that ${f_n(x_0)}$ converges for some point $x_0$ on $[a,b]$. If ${f_n'}$ converges uniformly on $[a,b]$, then ${f_n}$ converges uniformly on $[a,b]$, to a function f, and $$f'(x) = \lim_{n \rightarrow \infty} f_n'(x) \; (a\leq x\leq b)$$
증명
$\epsilon>0$이 주어졌다고 해봅시다.
우리가 앞선 포스팅에서 열심히 증명한 Cauchy sequence를 사용해보겠습니다. Statement의 가정에서처럼 $f_n(x)$는 $x_0$에서 pointwise converge합니다. 그러므로 적당한 $N1$을 택하고 그 $N1$보다 같거나 큰 $n,m$들에 대해($n,m\geq N1$) $|f_n(x_0)-f_m(x_0)| \leq \frac{\epsilon}{2}$가 성립함을 알 수 있겠죠. - Cauchy Pointwise version.
이번엔 도함수에 Cauchy를 써봅시다. 현재 구간 $[a,b]$에서 증명을 하고 있습니다. 앞으로 우리는 MeanValue Thm을 사용할 것이기 때문에 $\frac{\epsilon}{2(b-a)}$에 대해 또 적당한 $N_2$를 택해봅시다. 위와 비슷하게 $N2$보다 큰 $n,m$들에 대해 $|f_n'(t)-f_m'(t)| \leq \frac{\epsilon}{2(b-a)}$ 가 성립하도록 $N_2$를 택합시다.
다음으로는 $N$을 $max(N1,N2)$로 새롭게 설정합시다. 그러면 새롭게 설정한 $N$은 위의 두 부등식을 동시에 만족시키는 N이 되겠죠?
좋습니다.
이번엔 결론적으로 우리가 증명해야할 것을 상기해봅시다. 결국은 $|f_n(x)-f_m(x)| \leq \epsilon$임을 보이고 싶은겁니다.
여기서 우리는 $ |f_n(x)-f_m(x)| = |f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0) + f_n(x_0) - f_m(x_0)|$의 형식으로 식을 전개한 다음 $|f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0) + f_n(x_0) - f_m(x_0)| \leq |f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0)| + |f_n(x_0) - f_m(x_0)| $ 과 같이 삼각부등식에 의해 전개한 후 증명을 시도할 겁니다.
마지막 항의 가장 뒤의 식인 $|f_n(x_0) - f_m(x_0)|$는 Pointwise converge로 앞에서 끝냈습니다. 우리에게 남은건 $|f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0)|$를 처리하는 겁니다.
x_0를 대입하지 말고 $[a,b]$에서 임의의 $t$를 선택합시다.
이로부터 우리는 $|f_n(x)-f_m(x) - f_n(t) + f_m(t)|$의 범위를 정해보겠습니다.
먼저 mean-value thm에 대해 알아보죠. $[x,t]$구간에서(사실은 Compact Set일 때) 연속함수(Continuous function)가 있다고 해봅시다. 이 구간의 처음에서 끝을 연결한 기울기 즉, $\frac{f(t)-f(x)}{t-x}$에 대해 구간 내 어떤 $x'$이 존재해서 $f'(x')=\frac{f(t)-f(x)}{t-x}$ 라는 것이 mean-value thm입니다. 아래 그림은 그 시각화입니다.
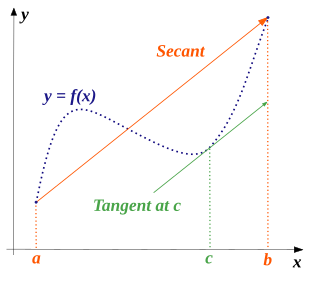
이 친구를 조금 더 응용하면 $|f(b)-f(a)| \leq (b-a)|f'(x)|$ 임도 쉽게 보일 수 있습니다. Rudin thm 5.19에 그 증명이 제시되어 있는데 $f(b)-f(a)$가 양수일 때와 음수일 때로 Case를 나누는 것이 더 직관적으로 보입니다.
$|f(b)-f(a)| \leq (b-a)|f'(x)|$를 우리의 식에 한 번 사용해보죠.
$|f_n(x)-f_m(x) - f_n(t) + f_m(t)|$에서 $b$를 $x$로 $a$를 $t$로 간주하고 $f_n-f_m$을 f로 생각합시다. 그러면 위의 부등식을 활용해서 $|f_n(x)-f_m(x) - f_n(t) + f_m(t)| \leq (x-t)|f'_n(x')-f'_m(x')|$ 으로 쓸 수 있습니다.
여기서 위의 $f'$의 범위인 모든 $x$에 대해 $|f'_n(x)-f'_m(x)| \leq \frac{\epsilon}{2(b-a)}$인 점을 사용하면(가장 처음에 있어용) $(x-t)|f'_n(x')-f'_m(x')| \leq (x-t)\frac{\epsilon}{2(b-a)}$로 쓸 수 있습니다. 이 때, $x-t \leq b-a$이므로 $(x-t)\frac{\epsilon}{2(b-a)} \leq (b-a)\frac{\epsilon}{2(b-a)} = \frac{\epsilon}{2}$입니다.
이제 $t$에 $x_0$를 대입하면 우리가 처리하고자 했던 $|f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0)|$를 처리한 셈이 됩니다.
즉, $ |f_n(x)-f_m(x)| \leq |f_n(x)-f_m(x) - f_n(x_0) + f_m(x_0)| + |f_n(x_0) - f_m(x_0)| \leq \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon$이고 by Cauchy,
$\therefore$ $f_n$은 uniformly continuous입니다.
자 이제 $f_n$이 수렴하는 $f$를 정의합시다. 즉, $f = \lim f_n$ 입니다.
또 $f$가 정의된 구간 $[a,b]$에서 point $x$를 fix합시다.
그리고 기울기 함수 두 개를 정의하겠습니다.
1. $\phi_n(t) = \frac{f_n(t)-f_n(x)}{t-x}$
2. $\phi(t) = \frac{f(t)-f(x)}{t-x}$
첫번째 sequence에 관한 기울기함수입니다. 지금 우리는 $x$ 하나를 정해둔 상태이고, $t$를 하나 정하고 $f_n$에서 기울기를 정했습니다.($n \geq N$)
두번째는 수렴한 함수인 f에 관한 기울기 함수입니다.
먼저 sequence에 대한 기울기 함수는 가정에서 differentiable이라고 했기 때문에 그 수렴값이 존재하고 이는 미분의 정의에 따라 $f_n'(x)$ 입니다. 즉, $$\lim_{t \rightarrow x} \phi_n(t) = f_n'(x)$$ 입니다.
또 $\phi_n$은 uniformly converge합니다.
왜냐하면 $|\phi_n(t) - \phi_m(t)| = |\frac{1}{t-x}||f_n(t)+f_m(t) - f_n(x) - f_m(x)|$ 이기 때문에 위의 증명처럼 $\frac{\epsilon}{2(b-a)}$보다 작음을 쉽게 보일 수 있습니다.(위의 증명에서 $(x-t)\frac{\epsilon}{2(b-a)}$ 부분을 가져와보세요!)
By Cauchy, uniformly converge하죠.($x \neq t$)
사실 좀 쉽게는 $f_n$이 uniformly converge하는 것을 보였기 때문에 그냥 $\lim$를 씌워서 바로 보일 수도 있습니다 ㅋㅋ
그 converge하는 함수는 $\phi(t)$가 될 겁니다. $\lim$ 씌워보면 자명합니다.
이제 우리는 $$\lim_{n \rightarrow \infty} \phi_n(t) = \phi (t)$$라는 사실을 알고 있습니다.
다음으로는 양변에 $\lim_{t \rightarrow x}$를 씌워보겠습니다.
우리가 증명없이 사용할 사실이 하나 있는데 Rudin thm 7.11의 $f$가 uniformly converge하다면 $$\lim_{t \rightarrow x} \lim_{n \rightarrow \infty} f_n = \lim_{n \rightarrow \infty} \lim_{t \rightarrow x} f_n$$ 이라는 사실입니다. 중요한데 따로 포스팅하도록 할게요.
다시 본론으로 넘어가면 $ \lim_{t \rightarrow x} \phi (t)= \lim_{t \rightarrow x} \lim_{n \rightarrow \infty} \phi_n(t)$가 된 것이고
$\lim_{t \rightarrow x} \lim_{n \rightarrow \infty} \phi_n(t) = \lim_{n \rightarrow \infty} \lim_{t \rightarrow x} \phi_n(t)$ 이 되며(Rudin thm 7.11)
$\lim_{t \rightarrow x} \phi_n(t) = f_n'(x)$ 이기 때문에(미분의 정의 + 미분 가능 가정)
$\lim_{t \rightarrow x} \lim_{n \rightarrow \infty} \phi_n(t) = \lim_{n \rightarrow \infty} f_n'(x)$입니다.
그런데 $\lim_{n \rightarrow \infty} \phi_n(t) = \phi(t)$ 이므로 (uniform convergence)
$\lim_{t \rightarrow x} \phi(t) = \lim_{n \rightarrow \infty} f_n'(x)$입니다.
여기서 $\lim_{t \rightarrow x} \phi(t)$는 다시 $f$의 미분인 $f'$이죠?
즉, $f' = \lim_{n \rightarrow \infty} f_n'(x)$라고 할 수 있겠습니다.
$\therefore$sequence의 미분의 극한은 수렴하는 함수의 미분입니다.
결론
우리는 드디어 Sequence의 합이 uniformly converge함을 확인하는 법과 Sequence의 미분의 극한이 수렴하는 함수의 미분이 되게 하는 법을 알았습니다. 이걸 지금까지 한 이유는 Series를 잘 정의하고 그 미분도 Sequence를 기반으로 잘 정의하기 위함이었습니다.
다음 포스팅에서는 일반적인 Series에 대해 수렴성을 잘 정의하고 특수한 Series인 Power Series에 대해 알아봄으로 m.g.f의 미분가능성에 대해 알아보도록 합시다.
'수리통계를 위한 해석학' 카테고리의 다른 글
| 찍먹 측도론2 Carathéodory's extension theorem and proof (0) | 2024.07.08 |
|---|---|
| 찍먹 측도론 Introduction(measure theory) (0) | 2024.07.05 |
| Moment Generating Function의 미분가능성? 3(feat. Power Series) (0) | 2024.06.23 |
| Moment Generating Function(m.g.f,적률생성함수)의 미분가능성? 1(feat. Uniform Convergence) (2) | 2024.06.21 |
| Moment Generating Function(m.g.f,적률생성함수)의 존재범위는? (2) | 2024.06.18 |