https://www.acmicpc.net/problem/7578
들어가는말
오랜만에 쭉 기억하고 싶은 문제가 있어 포스팅하게 되었습니다~
1년 반 전에 1615번 교차개수세기라는 문제를 풀었었습니다.
그 때 답지를 보지 않고 풀고 싶어서 공부하고 공부하다가 6개월만에 화장실에서 떠오른 번뜩이는 아이디어로 풀었던 기억이 있어요 ㅎㅎ
그 때는 누적합의 아이디어로 풀었었습니다.
한동안 잊고 살다가 이 문제를 발견했네요. 그 문제와 완전히 동일하고 조금 현실의 문제처럼 둔갑을 하고 있을 뿐입니다.
오랜만에 풀어보고자 접근했구요.
성장한 저는 Fenwick Tree로 이 문제를 풀어보았습니다.
서론이 길었네요. 바로 시작해봅시다.
문제 및 입출력

풀이
이 문제는 Bipartite graph의 교차 개수를 세는 문제입니다.
1. 교차의 이해
여기서 교차를 정의해봅시다.
각 node에 이름을 붙여줄게요!
입력으로 받는 노드 중 첫번째 줄에
$x_1,x_2,x_3...x_n$라는 이름을,
두번째 줄에
$y_1,y_2,y_3...y_n$라는 이름을 붙여줍시다.
그러면 공장의 한쪽의 기계들에는 $x$라는 이름이 반대쪽에는 $y$라는 이름들이 붙었네요.
다음은 예시입니다.
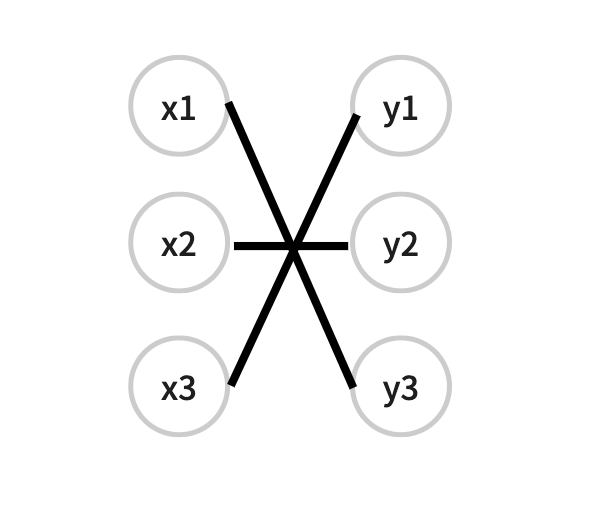
이 때 교차란 무엇이냐.
어떤 x를 선택했다고 합시다.
이 때 그 x보다 작은 x node들도 있고 큰 x node들도 있겠죠?작은 x들에 대응되는 y가 앞서 선택한 x의 y값보다 큰 경우!
큰 x들에 대응되는 y가 앞서 선택한 x의 y값보다 작은 경우!
교차하게 됩니다.
예를 들어!
위의 그림에서 $x_2$보다 작은 $x$는 $x_1$이죠? $x_1$은 $y_3$에 대응 되는데 이는 $x_2$에 대응되는 $y_2$보다 크죠?
그러면 자연스럽게 교차하게 됩니다.
$x_3$에 대한 case는 여러분에게 맡겨두겠습니다 ㅎ
위의 정의에서 우리는 핵심 아이디어를 얻을 수 있습니다.
한 edge(간선) 기준으로 위 아래 교차하는 선분들을 다 구해서 더해주자!
2. 근데 겹칠걸? 어떻게 처리할까
그런데 교차하는 선분들은 겹치겠죠? 그러니까 가장 첫 $x_i$에 대해 교차하는 선분을 구할 때 그 $x_i$보다 작은 $x$들에 관해서만 교차하는 수를 계산해주면 됩니다.
그러면 $x_i$보다 큰 $x$들과 겹치는 수는 어떻게 셀까요?
"쉽게는 $x_i$보다 큰 그 node들을 계산할 때 자연스럽게 세지게 된다." 정도로만 설명을 드리겠습니다.
한번 제가 말씀드린 방법으로 직접 세어보세요! 이해가 갈 겁니다!
사실 이 방법에는 조금 문제가 있습니다.
그냥 접근하면 당연스럽게 시간복잡도가 $O(n^2)$입니다.
그래서 우리는 Fenwick tree를 사용해서 이를 줄여봅시다.
3. Fenwick tree를 어떻게 쓸건데?
Fenwick tree는 구간합을 계산하기에 매우 유리한 자료구조입니다.
그런데 이 문제에 어떻게 적용할 수 있을까요??
저는 종만북이라는 책에서 삽입정렬의 시간을 재는데에 Fenwick tree를 사용한 예제를 본 적이 있습니다.
https://algospot.com/judge/problem/read/MEASURETIME
위의 문제입니다.
이 때, Fenwick tree를 처음부터 한 번에 다 계산하는 것이 아니라, 새로운 값이 들어오면 그에 대해 한 번 sum을 구하고 그 값을 새로이 update해주는 방식을 취합니다.
즉, update와 sum의 시간복잡도가 $O(log(n))$이므로 n개의 원소에 대해 $O(nlog(n))$의 시간복잡도를 가지게 할 수 있습니다.
이 문제에도 위의 아이디어를 적용해봅시다.
우리에게 Fenwick tree가 있다고 해봅시다. 모든 tree의 값은 초기에는 0입니다.
우리는 각 $x$들을 한 번씩 돌면서 이 Fenwick tree를 update할겁니다.
어떤 node $x$에 대해 Fenwick tree에는 그 $x$보다 작은 node들의 y값들의 구간합들이 저장했습니다.
예를들어 위의 예시에서 우리가 $x_3$를 보고 있다고 합시다.
$x_3$보다 작은 $x$는 $x_1,x_2$가 있고 이 x들에 대응되는 y값들에 대해
우리는 [0,1,1]이라는 값을 arr에 저장해둔 것입니다.
이 arr를 Fenwick tree로 만든 그 tree를 들고 있을 겁니다.
그리고 이 tree에 대해 현재 내가 보고 있는 $x$에 대응되는 $y$보다 큰 $y$들의 개수를 계산해주면됩니다.
Fenwick tree의 sum함수를 통해서 말이죠.
예시에서는 $x_3$에 $y_1$이 대응되기 때문에 1보다 큰 $y_2$,$y_3$에 대응되는 수 1+1 =2를 sum함수가 return할겁니다.
그리고 이 행위를 모든 $x_1,x_2,x_3...x_n$ 마다 반복해주고 그 결과를 한 변수에 저장하여 출력한다면 답이 되겠습니다.
구현
맨 처음에는 각 기계들의 번호를 순서대로 1번 2번...N번 까지 matching 해주었습니다. mapping 이라는 이름을 가진 dictionary로 구현됩니다.
그러면 $y$값들이 들어왔을 때 그 $y$가 몇 번째 x와 matching되는지 손쉽게 알 수 있습니다.
이를 converted에 저장해줍니다.나머지는 위의 설명한 과정입니다. $x$를 하나씩 돌면서 Fenwicktree를 통해 그에 대응되는 y에 대해 y+1~N까지의 합을 계산해주고 그 y를 update해줍니다.
import sys
N = int(sys.stdin.readline())
arr = list(map(int,sys.stdin.readline().split()))
mapping = {val : (idx+1) for idx,val in enumerate(arr)}
arr_2 = list(map(int,sys.stdin.readline().split()))
converted = [mapping[arr_2[i]] for i in range(N)]
tree = [0]*(N+1)
#현재의 y보다 큰 y를 가진 기계들의 수
def sumation(y):
ans = 0
while y>0:
ans += tree[y]
y -= (y&-y)
return ans
def update(y):
while y<len(tree):
tree[y] += 1
y += (y&-y)
ans = 0
for i in range(N):
cur = converted[i]
ans += (sumation(N) - sumation(cur))#ith 기계의 y값.
update(cur)
print(ans)끝맺음
제가 정말 예전에 오래 고민해서 풀었던 문제입니다. 그 때의 아이디어는 잊은 채로 시작했는데요.
이번엔 한 20분도 안걸려서 풀었네요 ㅎ
제겐 정말 소중한 문제입니다.
여러분도 한 번 두 문제 모두 풀어보시길 바랍니다 :)
'Baekjoon' 카테고리의 다른 글
| 백준 21909 Divisible by 3(Python) (2) | 2023.10.02 |
|---|---|
| 1725번 히스토그램(Python,스택) (0) | 2023.06.05 |
| 1520번 내리막길(dps+dp) (0) | 2023.06.04 |
| 25823번 조합의 합의 합 (0) | 2023.06.01 |
| 17298번 오큰수(DP,Backtracking) Python (1) | 2023.05.31 |

