선형대수_행렬곱에 대한 직관적 이해
1. matrix product에 대한 이해
matrix product
- matrix는 연립방정식을 풀기 위한 것이 주목적
- AX = B의 형태를 matrices와 vector의 꼴로 나타내면 자연스럽게 matrix product의 형태가 나온 방식을 알 수 있음.
- 이 때 m×n matrix A,n×k matrix B를 곱한 AB는 계수를 공유하는 연립방정식을 의미
$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix},B = \begin{pmatrix}
x_1 & x_2 \\
y_1 & y_2
\end{pmatrix}$의 곱 AB는
$ax_1+by_1,ax_2+by_2,cx_1+dy_1,cx_2+dy_2$의 4개의 방정식을 행렬로 표현한 것
matrix product의 종류
- 내적 표현법 $\begin{pmatrix} A_1^T\bf{b_1} \ A_2^T\bf{b_2} \end{pmatrix}$=$\begin{pmatrix} A_1 \ A_2 \end{pmatrix}\begin{pmatrix}
\bf{b}_1 & \bf{b}_2
\end{pmatrix}$ - Rank1 matrix 표현법 $\begin{pmatrix}
\bf{b}_1 & \bf{b}_2
\end{pmatrix}\begin{pmatrix} A_1 \ A_2 \end{pmatrix}$= $\bf{b}_1A_1+\bf{b}_2A_2$ - Rank1 matrix 표현법을 응용한 vector 표현법(위의 식의 $A_1$을 $x_1$으로 $A_2$를 $x_2$로 고치면 됨.
2. rowspace와 nullspace에 대한 이해
span
vector들로 만들수 있는 공간
ex) $\begin{pmatrix}
1 \\ 2
\end{pmatrix}$가 span 할 수 있는 것은 직선. $\begin{pmatrix}
1 \\ 2
\end{pmatrix}*x$ 가 나타내는 자취와 같음.
$\begin{pmatrix}
1 \\ 2
\end{pmatrix},\begin{pmatrix}
2 \\ 3
\end{pmatrix}$처럼 lineary independent한 두 vector가 span 하는 영역은 평면
row space
어떤 행렬 A에 대해 그 row vector들이 span 하는 space
null space
$A\bf{x}=\bf{0}$ 을 만족하는 $\bf{x}$들이 span하는 space
row space와 null space는 수직이다.
$A\bf{x}=\bf{0}$이면 $\bf{0} = \begin{pmatrix} A_1^T\bf{x}\\A_2^T\bf{x}\\...\\A_n^T\bf{x}\end{pmatrix}$이다. 이 때 $A_n^T\bf{x}$ = 0이므로 $\bf{x}$는 $A_n$과 내적이 0이고 즉 모든 row vector들과 수직이라고 할 수 있다.
어떤 null space의 vector를 꺼내오자. 그 vector는 row space의 모든 vector와 내적이 0이다.(row space의 vector는 row vector의 linear combination으로 이루어지기 때문)
즉, null space는 row space에 수직이다.
row_rank(A)+null(A) = n,(n은 n차원을 의미 in $\bf{R}^n$)
어떤 row space가 있다고 하자. row space의 차원은 row rank와 같다.(linearly independent한 row vector들로 이루어지므로)
어떤 vector $\bf{x}$가 row space에 수직이라면 $A\bf{x}=\bf{0}$ 을 만족한다. 즉, null space에 속한다.
(제 증명이라 틀린 부분이 있을 수도 있어요 ㅎㅎ)
그렇다면 row_rank(A)+null(A) = n
증명)
모든 vector $\bf{x}$에 대해 row space의 vector와 null space의 vector로 쪼갤 수 있음을 보이자. 즉, row space의 vector와 null space의 vector의 linear combination으로 표현될 수 있음을 보이자.
- $\bf{x}$가 row space에 속한다고 하자
이미 row space의 vector의 linear combination으로 표현 된 것
- 속하지 않는다고 하자.
이 때 row space에 $\bf{x}$에 대한 어떤 projection이 존재한다.. 이를 $\bf{x}'$이라고 하자.
$\bf{x}-\bf{x}'$은 row space에 수직이다.즉, null space에 속한다.
결론적으로 $\bf{x}$는 $\bf{x}'$와 $\bf{x}-\bf{x}'$의 합으로 표현할 수 있고 두 vector는 각각 row space와 null space에 속한다. row space에 속한 vector는 row space의 basis로 null space의 속한 vector는 null space의 basis로 표현 가능하므로 모든 $\bf{x}$는 그 두 개의 basis vector들만 있으면 표현 가능하다.
즉, 두 basis vector들의 수의 합은 n이다.
∴Q.E.D.
row rank = column rank
직관적으로 판단 가능. row echelon form 에서 independent row들의 수와 leading 1들의 수가 같고 leading 1을 가지고 있는 column들끼리 linearly independent이기 때문.
leading 1 뒤의 element들은 leading 1 column으로 cut 가능
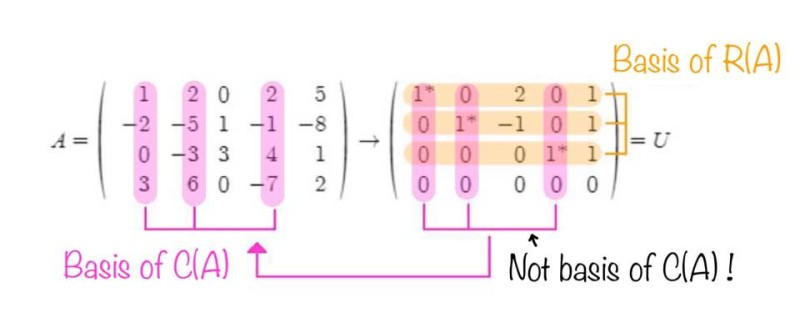
그림 출처) 네이버 블로그 프린키피아 Rank and nullity
∴ column_rank(A)+null(A) = n